Parallelogram law of vector addition Questions and Answers
Note: vectors are shown in bold. scalars are shown in normal type
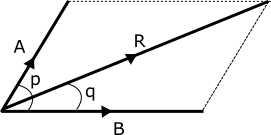
The diagram above shows two vectors A and B with angle p between them.
R is the resultant of A and B
R = A + B
This is the resultant in vector
R is the magnitude of vector R
Similarly A and B are the magnitudes of vectors A and B
R = √(A2 + B2 2ABCos p) or [A2 + B2 2ABCos p]1/2
To give the direction of R we find the angle q that R makes with B
Tan q = (A Sin p)/(B + A Cos q)
A vector is completely defined only if both magnitude and direction are given.
Question
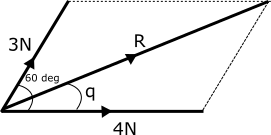
Two forces of 3 N and 4 N are acting at a point such that the angle between them is 60 degrees. Find the resultant force
Answer
Magnitude R of the resultant force is R = √(32 + 42 + 2 x 3 x 4 Cos 60 deg)
= √(9 + 16 + 12) = √(37 = 6.08 N
Direction of R is given by finding the angle q
tan q = (3 Sin 60 deg)/(4 + 3 Cos 60 deg) = 0.472
q = tan-1 0.472
= 25.3 deg
Thus R is 6.08 N in magnitude and is at an angle of 25.3 deg to the 4 N force.
Question
A car goes 5 km east 3 km south, 2 km west and 1 km north. Find the resultant displacement.
Answer
First we will make the vector diagram

O to A 5 km east
A to B 3 km south
B to C 2 km west
c to D 1 km north
Net displacement is OD
Along the horizontal direction: 5 km east - 2 km west = 3 km east
Along the vertical direction: 3 km south - 1 km north = 2 km south
OD = √(32 + 22 + 2 x 3 x Cos 90 deg)
= √(32 + 22)
= 3.6 km
tan p = 2/3
or p = tan-12/3 = 34 deg
Thus resultant displacement is 3.6 km, 34 deg south of east.
Rectangular components of a vector
To find the component of a vector along a given axis, we drop a perpendicular on the given axis from the vector

For example OA is the given vector. We have to find its component along the the horizontal axis. Let us call it x-axis. We drop a perpendicular AB from A onto the x-axis. The length OB is the component of OA along x-axis. If OA makes angle p with the horizontal axis, then in triangle OAB, OB/OA = Cos P or OB = OA Cos P.
Remember that component of a vector is a scalar quantity. If the component is along the negative direction, we put a (-) sign with it.)
Usually we resolve the vector into components along mutually perpendicular components.

OB is the x component OB = OA Cos p.
Similarly component along the vertical direction or the y axis is OC
OCAB is a rectangle.
So OC = AB
look at triangle OAB again,
AB/OA = Sin p
=> AB = OA Sin p = OC
Thus y component OC = OA Sin p.
Note that p is the angle with the horizontal axis.
Question
Find the x and y components of a 25 m displacement at an angle of 210 deg.

Answer
OA is the displacement vector. The angle with the horizontal axis is 210 deg - 180 deg = 30 deg
x component = OB = -25 Cos 30 deg = -21.7
y component = AB = -25 Sin 30 deg = -12.5 m
Note that each component is pointing along the negative coordinate direction and thus we must take it as negative.
Now we will solve a problem using the component method
Question
Find the resultant of the following two displacements: 2 m at 30 deg and 4 m at 120 deg. The angles are taken relative to the x axis.


Rx = 2 Cos 30 deg - 4 Cos 60 deg = - 0.268 m
Ry = 2 Sin 30 deg + 4 Sin 60 degg = 4.46 m
R = √(Rx2 + Ry2)
= √(-0.2682 + 4.462) = 4.47 m

tan q = Ry/Rx = 4.46/0.268
=> q = 86.6 deg
p = 180 deg - 86.6 deg = 93.4 deg