Circular Motion Gravitation Force Moment of Inertia
Question
A sphere shell has inner radius R, outer radius R, and mass M, distributed uniformly throughout the shell. Find the magnitude of the gravitational force exerted on the shell by a point particle of mass m located at a distance d from the center, outside the inner radius and inside the outer radius.
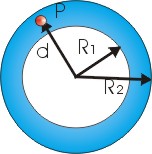
Paragraph
Hint
The mass of the spherical shell that will cause force will be mass located between the spheres of radius d and radius R1. As mass is distributed uniformly in the shell we can determine the density. Then we can find the force exerted.Answer
Mass of the sphere =
M
Point P is at a distance of d from the center and there is a particle of mass m located there.
The mass of the spherical shell that will cause force will be mass located between the spheres of radius d and radius R1.
That is mass of volume
4/3Πd3 - 4/3ΠR13 = 4/3Π(d3 - R13)
Mass is distributed uniformly in the shell. Thus density of the shell is
M/[4/3p(R23 - R13)]
Thus
M' = M/[4/3Π(R23 - R13)] x 4/3Π(d3 - R13) = [(d3 - R13)M]/(R23 - R13)
Thus force exerted on m is =
G.m.M' / d2
or